存在奇异值的非平稳谐波电流分析研究
孙辉
摘要:为了分析电力系统中存在奇异值的非平稳谐波电流,提出了一种小波包变换和快速傅里叶变换(FFT)综合算法,用小波包算法对谐波电流剔除奇异值和去除噪声后,对各个谐波频段进行重构和FFT运算,得到了非平稳谐波电流频谱特性和各次谐波的起止时刻,并和直接FFT算法进行了比较。结果表明,小波包变换和FFT综合算法能提高谐波电流分析的频谱精度,并能较准确地捕捉非平稳电流各次谐波的起止时刻,为有源电力滤波器(APF)补偿谐波电流提供依据。
关键词:奇异值;非平稳谐波电流;小波包变换;FFT
0 引言
随着电力电子技术的发展,电力系统中增加了许多非线性负载,使电网电流、电压发生畸变[1]。同时由于电力系统工程中设备运行状态千变万化,导致配电网中存在大量的非平稳信号。谐波和非平稳信号的叠加,进一步导致了电网波形的恶化。为了减小谐波的危害,必须通过算法监测谐波的成分[2]。目前用到的方法主要由以下几种:
1)基于瞬时无功功率理论的p、q运算方式和ip、iq运算方式,在实际应用中,ip、iq运算方式应用较多。但是对单相电路的监测算法比较复杂,不容易实现[3~4]。
2)快速傅里叶变换(FFT)算法,这是一种常用的谐波检测方法,但FFT算法只有频域分析功能,无法确定非平稳信号中突变点的发生时刻,并且对谐波的检测存在栅栏效应和频谱泄露现象,从而使检测出来的谐波幅值、频率和相位有较大误差[6~8]。
3)小波变换算法,此算法可灵活选取小波基函数,具有频域和时域分析功能,适用于时变的非平稳信号的检测与分析,但它只对每次分解的低频系数进行细分,而对高频系数不再分解,导致出现一定误差[9]。
4)小波包分解算法,它能够为信号提供一种更加精细的分析方法,通过把频带进行多层次的划分,小波包分解能够对多分辨分析中没有细分的高频部分进一步分解,并能根据被分析信号的特征,自适应地选择相应的频段,使之与信号频谱相匹配[10]。
根据以上各种方法的优劣,本文提出了一种存在奇异值的非平稳信号谐波分析研究,结合了小波包变换和FFT的特性,在消除奇异值和噪声的条件下,得到信号的谐波分量。并和直接FFT的结果进行了比较,结果表明,此综合方法可以提高频谱分析的精度,并且能够确定非平稳信号突变点的时刻,是一种有效的谐波监测方法,对有源电力滤波器中监测谐波电流做出补偿有一定的参考价值。
1 综合谐波分析算法
本文对有奇异值的非平稳信号谐波分析的综合算法步骤如下:
1)首先对信号进行小波包分析,利用其时域分析的特性找到奇异值发生时刻和非平稳信号突变点的起止时刻。
2)消除奇异点,并对要分析的谐波频率段进行整数次谐波重构。在这一步中,由于只对有效次谐波进行了重构,也进一步消除了加性噪声干扰。
3)然后结合FFT和小波包变换的频域特性,确定信号的频谱。
4)综合第一步谐波突变点的起止时刻和第三步的频谱结果,得到消除奇异点和去除噪声后的非平稳信号的频谱和突变时刻。
2 算例分析
根据GB/T 14549-1993《电能质量—公用电网谐波》中关于0.38KV系统公共联接点的全部用户向该点注入的谐波电流分量(方均根值)的最高允许值的规定,取谐波电流中3次,5次,7次,13次,15次谐波电流的允许值作为算例分析的谐波电流组成。构造了以下谐波电流函数:
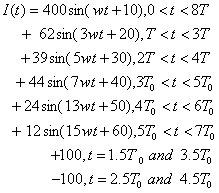 (1)
(1)
其中![]() ,f=50HZ,T0=0.02s,I(t)单位为A。
,f=50HZ,T0=0.02s,I(t)单位为A。
由式(1)可只,I(t)由基波分量、3次、5次、7次、13次、15次谐波分量、某时刻的奇异值分量组成。I(t)和其各谐波分量波形如图1所示。可以看出,谐波电流中突变点出现在t=0.02s、0.04s、0.06s、0.08s、0.10s、0.12s、0.14s时刻,奇异值出现在t=0.03s、0.05s、0.07s、0.09s时刻。

图1 I(t)和其组成分量
Fig.1 I(t) and its composition
对谐波电流的采样频率fs=3200HZ,采样周期Ts=1/fs,采样时间T=8T=0.16s。对I(t)进行FFT分析结果如图2所示。
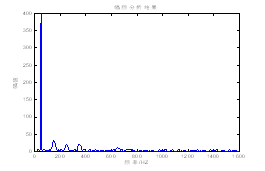
图2 FFT谐波分析结果
Fig.2 The harmonic analysis results with FFT
首先用“db20”小波进行4层小波包分解和重构,小波包分解树结果如图3所示:
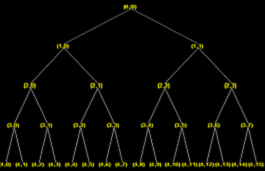
图3 4层小波包分解树结构
Fig.3 The tree structure of Wavelet packet transform
由采样定理可知,fs=3200HZ时,可分析的带宽为0-1600HZ,小波包分解树中各节点对应的带宽如表1所示。
表1 小波包分解树各节点带宽
Tab.1 The Bandwidth of each node
|
0,0 |
1,0 |
1,1 |
2,0 |
2,1 |
2,2 |
2,3 |
3,0 |
3,1 |
3,2 |
3,3 |
3,4 |
3,5 |
3,6 |
3,7 | |
|
0-1600 |
0-800 |
800-1600 |
0-400 |
400-800 |
800-1200 |
1200-1600 |
0-200 |
200-400 |
400-600 |
600-800 |
800-1000 |
1000-1200 |
1200-1400 |
1400-1600 | |
|
4,0 |
4,1 |
4,2 |
4,3 |
4,4 |
4,5 |
4,6 |
4,7 |
4,8 |
4,9 |
4,10 |
4,11 |
4,12 |
4,13 |
4,14 |
4,15 |
|
0-100 |
100-200 |
200-300 |
300-400 |
400-500 |
500-600 |
600-700 |
700-800 |
800-900 |
900-1000 |
1000-1100 |
1100-1200 |
1200-1300 |
1300-1400 |
1400-1500 |
1500-1600 |
则基波、3次、5次、7次谐波、13次、15次谐波落在节点(4,0)、(4,1)、(4,2),(4,3)、(4,6)、(4,7)内,画出图形如图4所示。
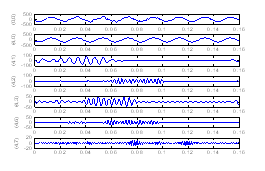
图4 小波包基波、各次谐波分析结果
Fig.4 The analysis results of base and harmonic current
图4中各节点波形可以反映出基波和各次谐波的频率。对非平稳信号突变点时刻中,对13次和15次谐波突变点没有精确地分析出来。
但从节点(1,1)和(2,2)分析中,可以很好体现出各次谐波的突变点和奇异值发生时刻。如图5和图6所示。
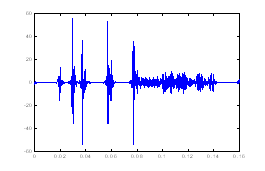
图5 节点(1,1)分析结果
Fig.5 The analysis results of (1,1)

图6 节点(2,2)分析结果
Fig.6 The analysis results of (2,2)
节点(1,1)分析的频带较宽,对细节信号(高频部分)分析不足,但可以体现出低次谐波的突变点:在t=0.02s、0.04s、0.06s和0.08s附近出现了突变点,结合图4可知所代表的是3次谐波突变起止点、5次谐波突变起止点、7次谐波突变起点。在t=0.03s、0.05s附近出现了奇异值。
节点(2,2)分析的频带相对较窄,对细节信号(高频部分)体现完整:在t=0.08s、0.1s、0.2s、0.14s附近出现了突变点,结合图4可知所代表的是7次谐波突变止点、13次谐波突变起止点、15次谐波突变起点。在t=0.03s、0.05s、0.07s、0.09s附近出现了奇异值。
然后对图4中基波、各次谐波对应的节点数据进行FFT分析,得到基波、各次谐波分量。并和直接FFT分析结果比较,列表2。可以看出,本文方法提高了谐波电流的频谱分析精度。
表2 直接FFT和本文算法结果比较
Tab.2 The comparison of direct FFT and integrated algorithm
|
频率/HZ |
150 |
250 |
350 |
650 |
750 |
|
FFT算法 |
148.7 |
248.5 |
342.1 |
647.7 |
747.5 |
|
本文算法 |
149.7 |
249.7 |
349.7 |
649.6 |
749.5 |
|
幅值/A |
62 |
39 |
44 |
24 |
12 |
|
FFT算法 |
61.2 |
39.52 |
43.19 |
23.56 |
12.9 |
|
本文算法 |
62.83 |
40 |
43.7 |
24.06 |
12.217 |
3 结论
1)本文所提出的谐波分析综合算法,对有奇异值的非平稳谐波电流有较好的分析效果,可以得到奇异值发生时刻和各次谐波的起止时刻。
2)小波包分析剔除奇异点和去除噪声后,再对小波包特定节点频段进行FFT,可以提高频谱分析的精确度。
3)本文为有源电力滤波器监测谐波电流提供了一种精确地算法,不仅能分析谐波电流的频谱,而且能确定各次谐波电流产生的消失的时刻。为有源电力滤波器的补偿谐波次数、幅值和补偿时刻提供了理论依据。但对算法的运算时间有待考证。
参考文献
[1] 杨际峰.小波包变换在电力系统谐波检测中的应用研究[J].制造业自动化,2010,(15):181-183.
[2] 黄涛.基于DSP的并联型有源电力滤波器的研究[D].清华大学,2004.
[3] 石新春,杨京燕,王毅.电力电力技术[M].北京:中国电力出版社,2006:171-177.
[4] 梁志瑞,叶慧强,赵飞.电力系统谐波状态估计研究综述[J].电力系统保护与控制,2010,38(15):157-160.LIANG.
[5] Vlahinic, Dalibor, Dubravko. Measurement and analysisof harmonic distortion in power distribution systems[J].Electric Power Systems Research,2009,79(7):1121-1126.
[6] 肖湘宁.电能质量分析与控制[M].北京:中车电力出版社,2004:25-35.
[7] 梁玉娟,李群湛,赵丽平.基于小波分析的电力系统谐波分析[J].电力系统及其自动化学报,2003,(06):67-70.
[8] Sanoso S, Grady W M, Powers E J, et al.Characterization of distribute power quality events withFourier and wavelet transforms[J].IEEE Trans on PowerDelivery,2000,15(1):247-254.
[9] 刘明才.小波分析及其应用[M].北京:清华大学出版社,2005.88-108.
[10] 周伟.MATLAB小波分析高级技术[M].西安:西安电子科技大学出版社,2006:9-10.




























































