HHT算法中电压中断与电压暂降识别研究

摘要：针对希尔伯特黄变换(HHT)具有无法有效识别电网电压暂降和电压中断两种状态的局限性，提出了频率比较法在电网电压暂降和电压中断识别中的应用。由仿真结果可知，电网电压暂降幅度不同时，HHT算法的仿真结果中IMF分量的幅值和瞬时频率波动情况也不完全相同。基本规律是电压暂降幅值越大，暂降期间IMF分量的幅值平均值越小，瞬时频率波动越大；电压中断期间，IMF分量的瞬时频率几乎为0，幅值平均值较大。利用电压中断期间和暂降期间IMF分量瞬时频率的不同特点可以有效识别这两种状态。算例结果验证了该方法的实用性。

关键词：HHT；电压暂降；电压中断；识别；频率比较法

中图分类号：TM743         文献标志码：A

0 引言

近年来，电力电子技术的发展和电力系统中非线性负荷的增加导致电网电压波动频繁[1]。此外，光伏发电、风力发电等分布式电源大规模接入电网也给电网带来了各种扰动，影响电能质量[2-3]。电压暂降和电压中断是两种常见的电能质量问题，电网电压暂降主要包括以下3种情况；1.输配电系统中发生瞬时性故障时各母线将出现不同程度的电压暂降；2.大容量感应电机启动时，定子电流明显增大，从而引起所接母线发生电压暂降；3.雷击时造成绝缘子闪络使保护装置动作，从而导致供电电压暂降[4]。

为了有效检测出电网电压的变化情况，相关领域的专家提出了希尔伯特黄变换（HHT）在电网电压变化检测中的应用。相对于其他信号处理方法，HHT具有自适应性强，能处理非线性非平稳信号，不受Heisenberg测不准原理制约等优点，得到了广泛应用[5-10]。HHT通过分析IMF分量的频率/时间变化曲线实现对电压变化时刻的检测，通过分析其幅值/时间变化曲线来检测电压变化幅度。仿真结果表明，由仿真结果可知，电压暂降幅值越大，暂降期间IMF分量的幅值平均值越小，瞬时频率波动越大；电压中断期间，IMF分量的幅值平均值反而较大，导致HHT无法有效识别电压中断和电压暂降两种状态。

针对此问题，结合电压中断时IMF分量瞬时频率的特征，提出频率比较法在识别电压暂降与电压中断中的应用。对电压变化区间内IMF分量的瞬时频率进行采样，求取采样值的平均值，通过瞬时频率平均值的大小识别出电压暂降和电压中断两种状态。

1 HHT简介

希尔伯特黄变换(HHT)是由美籍华人Norden E. Huang所提出来的一种全新的信号处理方法，该方法由经验模态分解（EMD）和希尔伯特变换两部分组成[11]。通过EMD分解将任何复杂信号分解成有限个固有模态函数IMF，再根据希尔伯特变换求出每一个IMF的瞬时频率和瞬时幅值。

1.1 EMD分解过程

先根据信号的极大点与极小点求出其上包络及下包络的平均值

            （1） 

然后求取与的差即为，即

                  （2） 

将作为原始数据，重复以上过程次，得到，直到满足IMF分量的条件为止。EMD的分解结果如式3所示。

     （3）

式中表示各个IMF分量，表示残余量。

1.2 希尔伯特变换

    对EMD分解得到的第个IMF分量进行Hilbert变换为

       （4）                    

其反变换为

       （5）                            

得到解析信号

（6）

其中，瞬时幅值，相位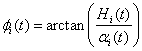。瞬时频率的计算公式为

      （7） 

2 仿真结果分析

本文对电压暂降情况中0.8Un、0.3Un以及0.1Un（Un表示电网额定电压）三种情况下的HHT结果进行了仿真分析，对电压中断也进行了同样的仿真分析。仿真结果如图1-4所示。

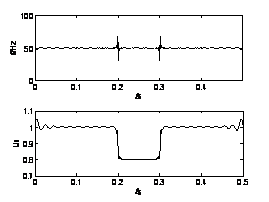
图1 电压暂降为0.8Un时HHT仿真图

Fig.1  Figure of simulation of HHT when 

the voltage sag is 0.8Un

图2 电压暂降为0.3Un时HHT仿真图

Fig.2  Figure of simulation of HHT when 

the voltage sag is 0.3Un

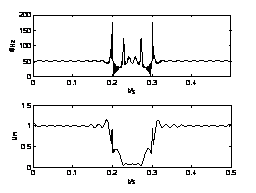
图3 电压暂降为0.1Un时HHT仿真图

Fig.3  Figure of simulation of HHT when 

the voltage sag is 0.1Un

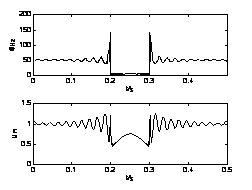
图4 电压中断时HHT仿真图

Fig.3  Figure of simulation of HHT of 

voltage interruption

从图1-3中可以定性分析出电网电压暂降幅度不同时，HHT算法的仿真结果中IMF分量的幅值和瞬时频率波动情况也不完全相同。基本规律是电压暂降幅值越大，暂降期间IMF分量的幅值平均值越小，瞬时频率波动越大。HHT算法根据IMF分量的频率/时间曲线可以有效识别出电压暂降发生的时刻，根据IMF分量的幅值/时间曲线可以定量计算出电压暂降的幅度。

分析图4仿真结果可知，电压中断以及电压恢复时刻可以方便地由IMF分量的频率/时间变化曲线中瞬时频率的变化情况求得。此时，针对IMF分量的幅值/时间变化曲线，用同样的求电压变化期间IMF分量幅值的平均值无法得到预想的结果，反而该值较大（从图4中可以定性看出），这是HHT在理论方面的缺陷所致。为了有效识别出电压暂降与电压中断两种状态，提出了频率比较法。

3 频率比较法简介

假设电网在时间段内发生电压中断，根据图4中频率/时间关系曲线可得两个电压突变时刻瞬时频率变化较大，其他时间频率相对稳定。对于电压暂降而言，在暂降时间段内，频率接近50Hz；而对于电压中断而言，在暂降时间段内，频率接近0Hz。对时间段内的频率进行等间距n点采样，这n个采样点的瞬时频率的平均值可由式8求得。

        （8）

假设设定频率门槛值，该值可以根据实际情况及经验值设定。若>,则判定为电压暂降；反之若<,则判定为电压中断。

根据图4中频率/时间关系图可得，电压突变时刻瞬时频率变化较大，而且时刻附近的频率波动也相对比较大，直接运用式8进行电压暂降和电压中断识别容易导致误判断。为了提高算法的可靠性，避免误判断，本文又提出采用延时来解决此问题，即对时间段内的频率进行等间距n点采样，然后求取平均频率并进行电压暂降和电压中断判断。延时可以根据实际经验进行选取，对此本文做了大量的仿真分析，结果发现取1-2ms时既可以提高算法的可靠性，又不至于牺牲算法的实时性。

为了验证上述方法的可行性，本文同样进行了算例验证，仿真中选取的频率门槛值为5Hz，具体结果见表1.

表1 电压暂降、中断判断结果表

Tab1.Table of result of voltage dip and interruption

4 结论

针对希尔伯特黄变换(HHT)具有无法有效识别电网电压暂降和电压中断两种状态的局限性，提出了频率比较法在电网电压暂降和电压中断识别中的应用。根据电压中断的仿真结果可知电压中断期间IMF分量的瞬时频率几乎为0，此特点有别于电压暂降，对中断期间IMF分量的瞬时频率进行等间距n点采样，求取采样频率的平均值，通过比较采样频率平均值与之前设定的频率门槛值的大小即可识别电压暂降和电压中断。算例仿真结果证实该方法的实用性。